Number of Paths on a Grid Map方格路徑上的路線數目

如圖所示，有一個 $4\times 5$ 的方格路徑，從 $A$ 點出發，只能向上或向右行，不能斜行，共有多少條到達 $B$ 的路徑呢？

我們先看一下有效路徑的例子：

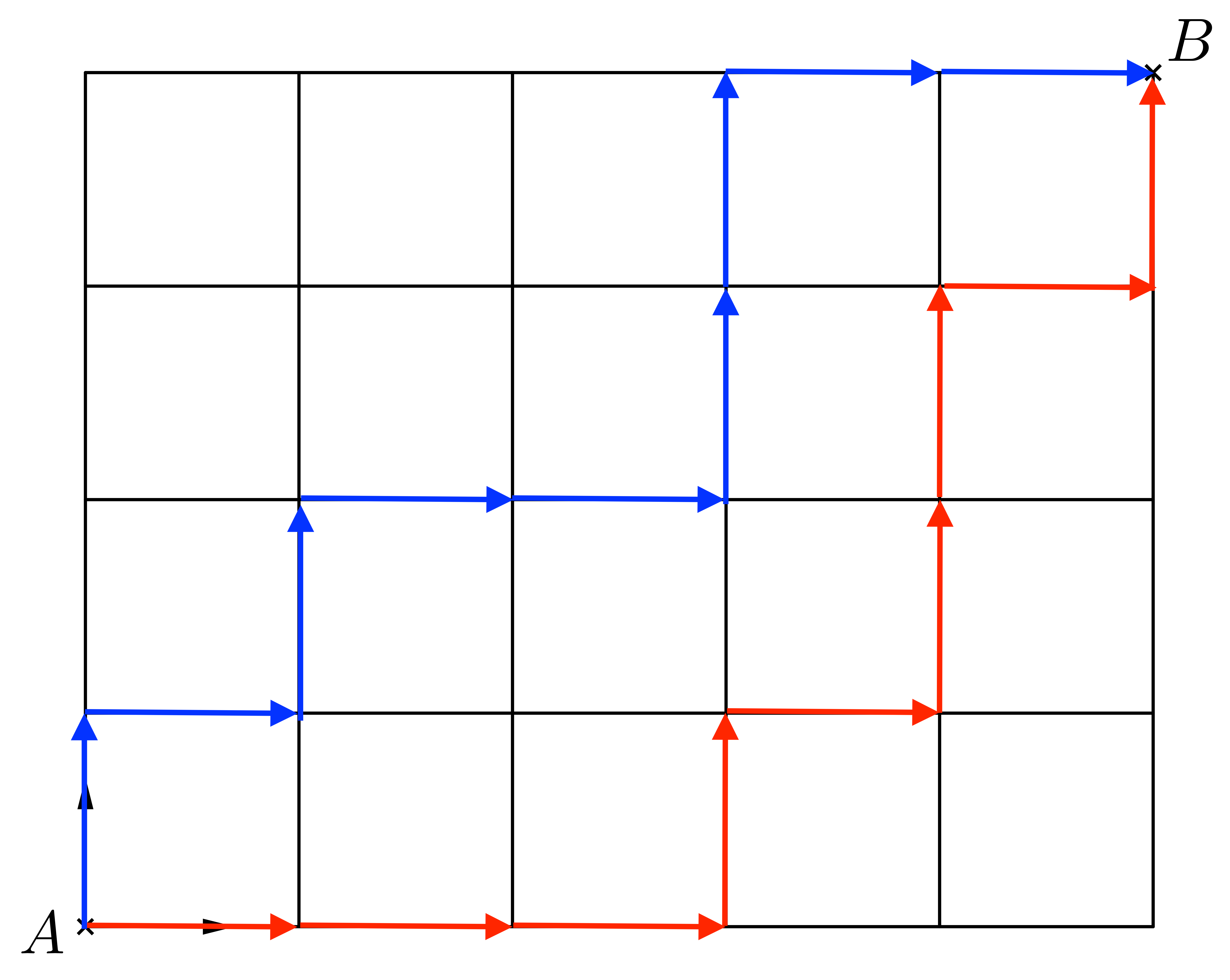
先試以符號表示上述兩個路徑：
藍色路徑：↑ → ↑ → → ↑ ↑ → →
紅色路徑：→ → → ↑ → ↑ ↑ → ↑

可推斷出每條有效的路徑都含有 4 個 ↑，5 個 →，總共需要 9 個步驟去完成一個有效的路徑。要數出所有有效路徑的數目，我們可以先想像有 9 個空格，代表著 9 個步驟：

_ _ _ _ _ _ _ _ _

由於每一個有效的路徑需要有 4 個 ↑，我們可以於 9 個空格中任意選出 4 格，放下 ↑。

_ ↑ _ ↑ ↑ _ _ _ ↑

其餘空格就必然是 →，所以只要我們選好哪四格放 ↑，就能找出一條有效的路徑：

→ ↑ → ↑ ↑ → → → ↑

所以一條有效的路徑其實是由一開始從 9 個空格中選擇了哪 4 格為 ↑ 而決定，所以有效路徑的數為 $C_4^9=126$ 。

一般而言，對於一個 $n\times m$ 的方格路徑，我們需要一開始從 $m+n$ 個空格中選擇了哪 $n$ 格為 ↑ 而決定，所以有效路徑的數為 $C_n^{m+n}$ 。

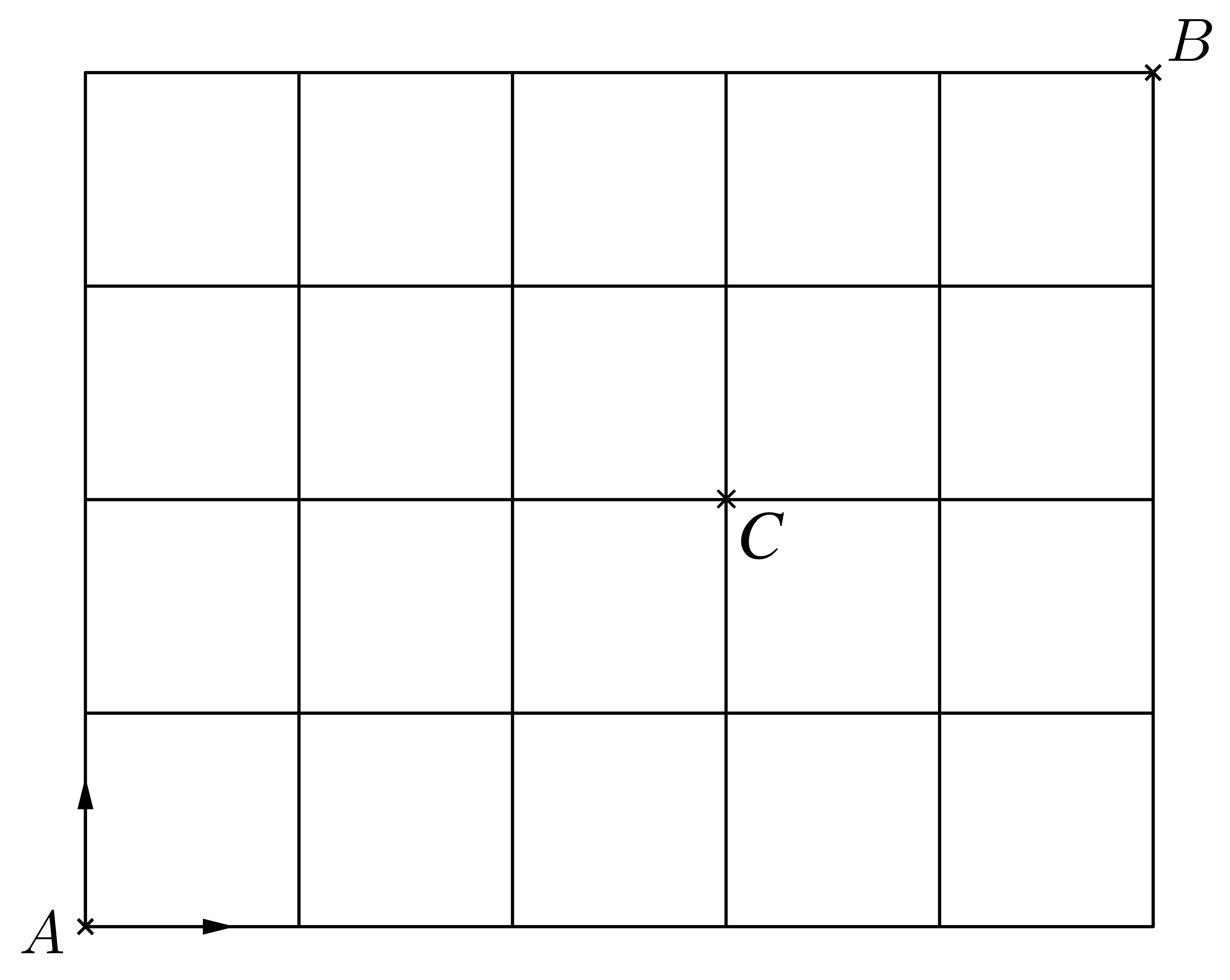
A man start moving from $A$ to $B$ and he can only go up or right, find the number of possible path if he needs to pass through $C$ .

一人從 $A$ 點出發去 $B$ ，他只能向上或向右行，問共有多少條通過 $C$ 的路徑呢？

Number of Paths on a Grid Map
方格路徑上的路線數目